大数法则与中心极限定理
引言
大数法则与中心极限定理在通信领域中发挥着重要的作用，故记录。
大数法则
定义
假设$X_1, X_2, \dots, X_n$是独立同分布变量（i.i.d），他们的期望是$\mu$，标准差是$\sigma$。令$\overline{X}_n$是$X_1, X_2, \dots, X_n$的平均值：
$$\overline{X}_n = \frac{X_1 + X_2 + \cdots + X_n}{n} = \frac{1}{n} \sum_{i=1}^nX_i$$
大数法则指出：随着$n$的增加，$\overline{X}_n$近似等于$\mu$的概率接近1，即$\overline{X}$依概率收敛于$\mu$（$\overline{X} \stackrel{P}{\longrightarrow} \mu$）。数学定义为：
$$\lim_{n \to \infty} P(|\overline{X}_n - \mu| < a) = 1$$
其中，$a$是任意正数。
举例
假设$X_i$代表的事件是抛硬币，1代表正面朝上，0代表反面朝上。所以，$X_i$ ~ Bernoulli(0.5)。根据大数定律，随着试验次数$n$的增加，$P(|\overline{X}-0.5| < a)$将接近1。给定$a=0.01$，相当于计算$P(0.49 \leq \overline{X} \leq 0.51)$的取值。
实验结果如下：
n = 10: 0.2460937
n = 100: 0.2356466
n = 1000: 0.49334
n = 10000: 0.9555742可以看出，随着$n$的增加，实验结果逐渐收敛于1。
应用
大数定律的一个应用是：频率直方图可以很好的近似概率密度函数（PDF）。
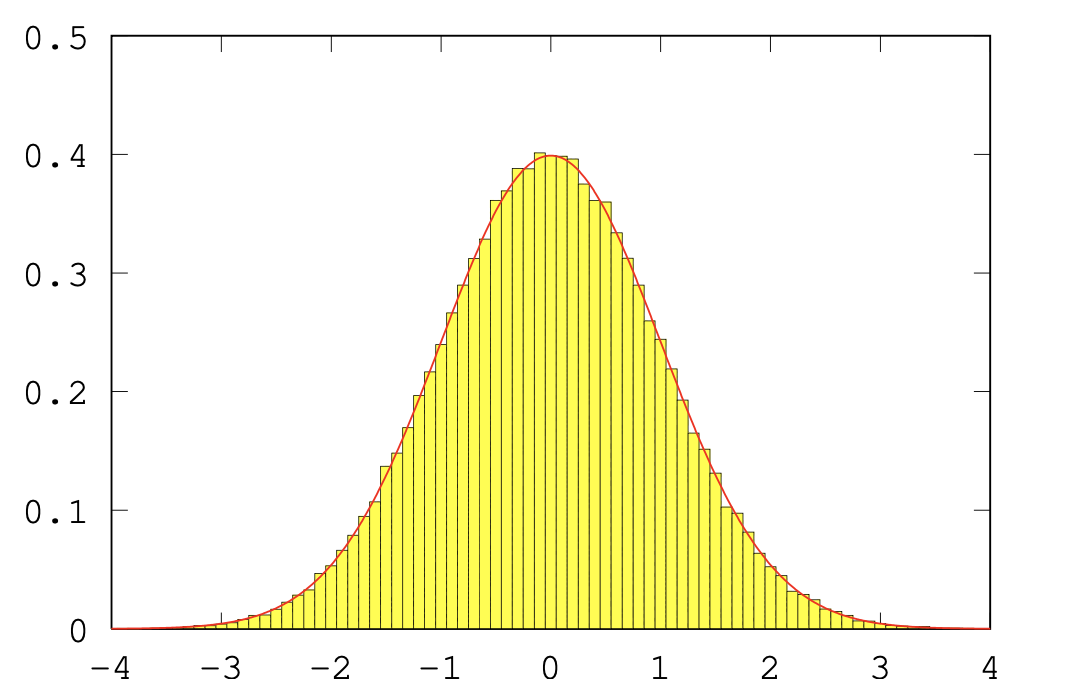频率直方图与PDF
中心极限定理
定义
假设$X_1, X_2, \dots, X_n$是i.i.d，他们的期望是$\mu$，标准差是$\sigma$。令$S_n = \sum_{i=1}^n X_i$，所以$\overline{X}_n = \frac{S_n}{n}$。
可以得到，
$$E[S_n] = n \mu, Var[S_n] = n \sigma^2$$
$$E[\overline{X}_n] = \mu, Var[\overline{X}_n] = \frac{\sigma^2}{n}$$
对$S_n, \overline{X}_n$进行标准化，标准化的结果可以用同一个变量$Z_n$表示：
$$Z_n = \frac{S_n - n\mu}{\sigma \sqrt{n}} = \frac{\overline{X}_n - \mu}{\sigma / \sqrt{n}}$$
中心极限定理说明，当$n$足够大时：
$$\overline{X}_n \approx N(\mu, \sigma^2/n) $$
$$ S_n \approx N(n\mu, n\sigma^2) $$
$$ Z_n \approx N(0, 1)$$
需要注意的是：
- $\overline{X}_n, S_n, Z_n$均服从正态分布；
- $Z_n$服从标准正态分布。
举例
下图展示了不同实验/采样次数$n$下，均匀分布的平均值的PDF的演化过程。$n$依次为：1，2，4，8，12。
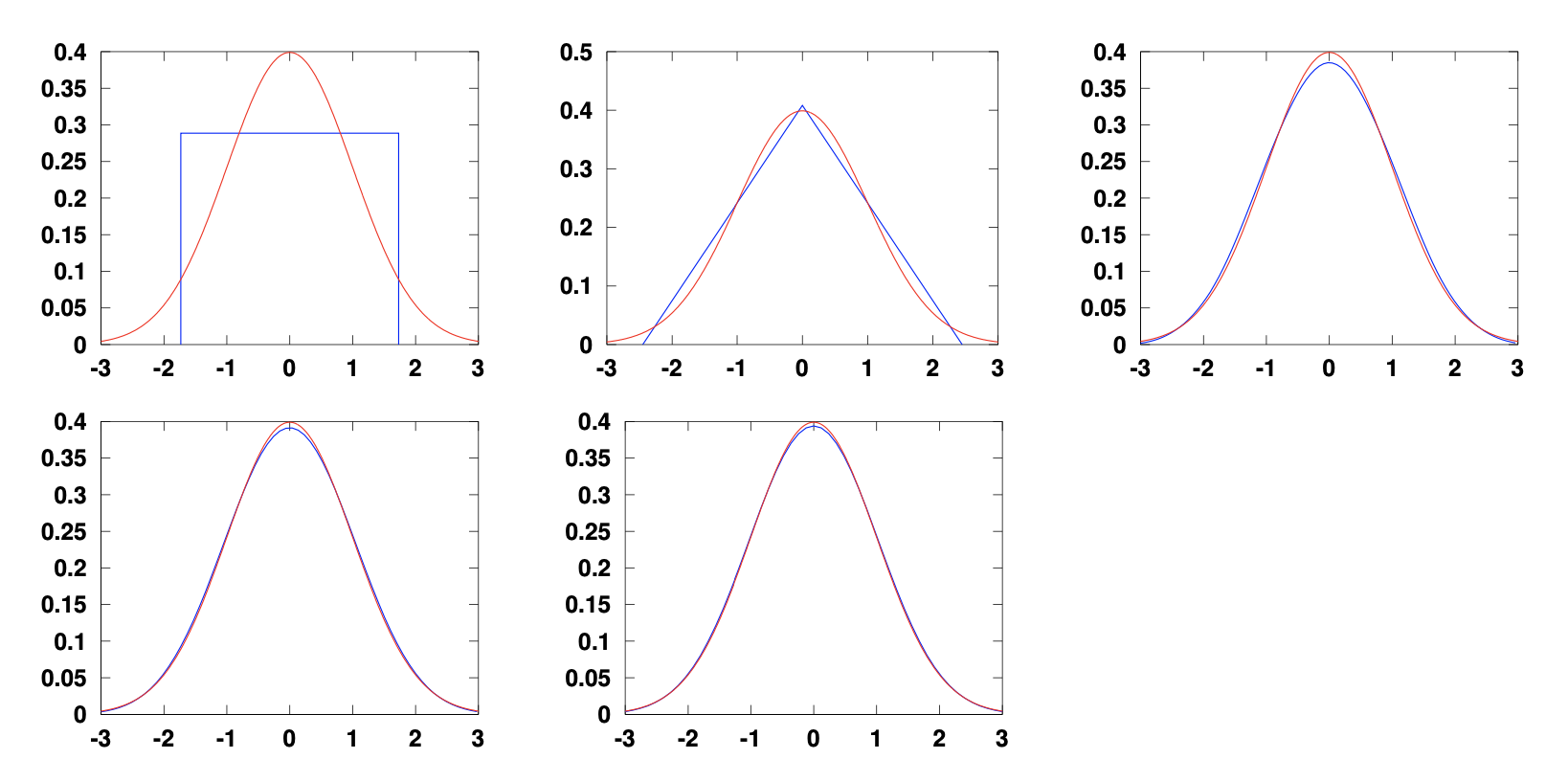均匀分布的平均值pdf
从上图结果可以看出，在12次时，平均值的pdf与正态分布的pdf基本重合，与中心极限定理的结论一致。
从这幅图的结果解读中心极限定理，可以认为：对于i.i.d随机变量，当数量越来越大时，靠近期望（中心）的事件发生的次数越来越多，pdf也逐渐向中心靠拢。
应用
中心极限定理的重要性在于，在分析某种i.i.d随机变量的累积效果时（期望、概率分布等），不用考虑其具体分布。只要$n$足够大，就可以当作正态分布处理。