KMP算法

Posted on Edited on In

引言

在帮小蒋查看编写的KMP算法错误时，又把KMP算法复习了一遍。在复习时，读到阮行止的知乎回答，受益匪浅，故记录。

简介

KMP算法是用来解决字符串匹配问题的一种算法。其中，字符串匹配问题可以解释为“字符串P是否是字符串S的子串？如果是，出现在S中的哪些位置”。在此类问题中，通常存在两个字符串：

  • S：主串
  • P：模式串

算法

Brute-Force

在解决字符串匹配问题时，首先想到的一种方法就是暴力算法：将模式串P与主串S进行从前至后的逐位比较。

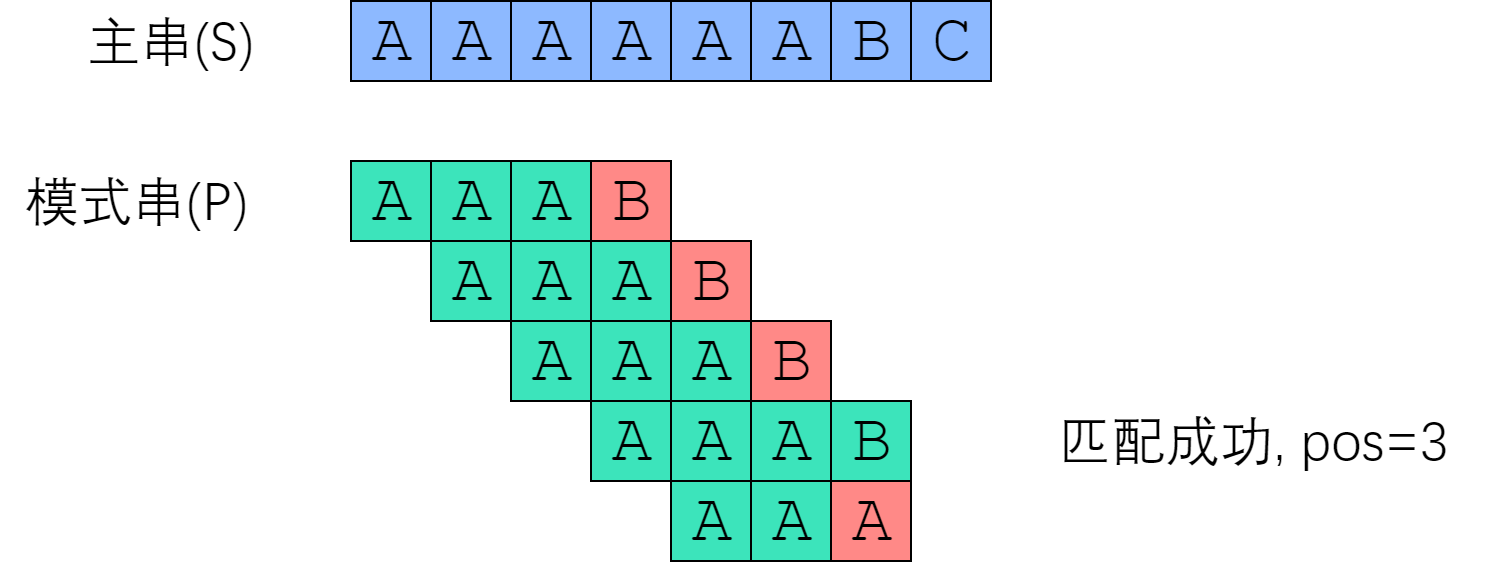Brute-Force示意图

下面给出一种基于C++的解法

Brute-Force
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int s_len = s.size();
int p_len = p.size();
int i, j, flag = 0;
while (i < s_len && j < p_len) {
	if (p[j] == s[i]) {
		i++;
		j++;
	} else {
		j = 0;
		flag++;
		i = flag;
	}
}
if (j == p_len) {
	cout << "true" << endl;
} else {
	cout << "false" << endl;
}

Brute-Force的优势在于思维量小，付出的代价则是运算量大。考虑最坏的情况，BF算法的复杂度是$O(mn)$，其中$m, n$分别代表S与P的长度。

Key idea：跳过不可能的距离

Brute-Force算法的高时间复杂度主要是因为没有利用到之前比较获得的结果。

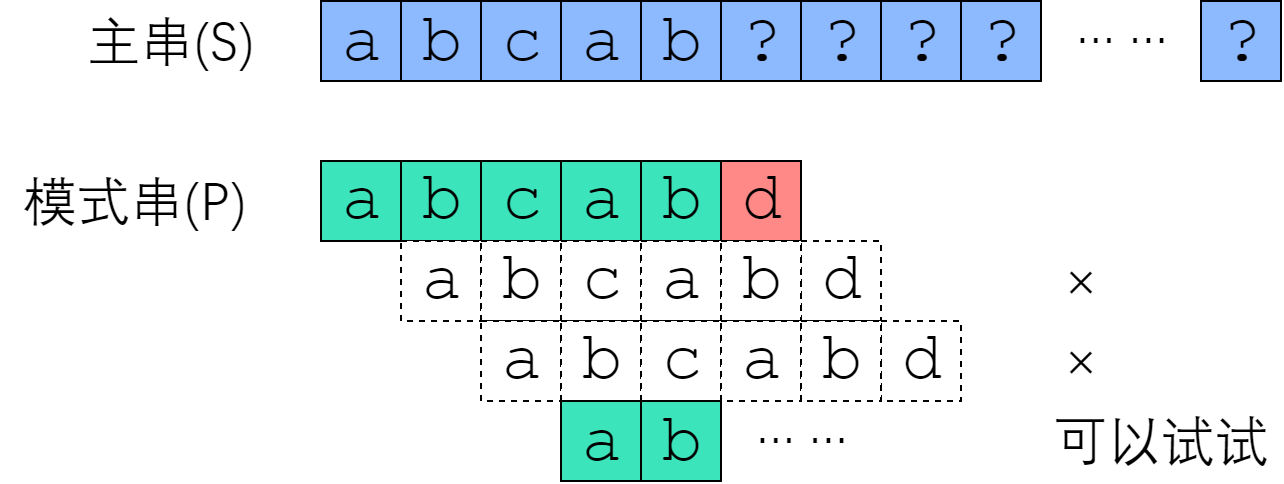无用比较示意图

如上图所示，第2、3次的比较其实是无用的。换言之，S[1]～S[2]其实是无用距离，可以直接跳过，令P[0]从S[3]开始进行匹配。那么，问题的关键就转变为如何跳过不可能的距离。

Next数组

跳过不可能的距离，需要借助于模式串P自身的特性。更具体地，该特性是指已匹配的字符串中前缀与后缀的重叠程度。为了观察记录该特性，需要构建next数组。

定义

下面给出next数组中元素的明确定义：

  • next[i]: P[0] ~ P[i] 这个子串中，前next[i]个字符与后next[i]个字符相等，且next[i]是符合前后缀相等条件的最大值。

构造思路

此处直接介绍快速构建next数组的方法。

考虑一般情况：

  • 已知：next[0] ~ next[i-1]，其中next[i-1] = k
  • 求解：next[i]

继续求解next[i]时，我们需要考虑的问题是：P[k] == P[i]是否成立。因此，需要分类讨论。

P[k] == P[i]

这是一种简单的情况。此时，可直接得到：next[i] = next[i-1] + 1 = k + 1。

P[k] != P[i]

这是一种较为复杂的情况。在介绍这种情况的求解思路之前，需要先做2个简明的定义：

  • 子串A：P[0] ~ P[k-1]，next[i-1]所对应的最长前缀
  • 子串B：P[i-k] ~ P[i-1]，next[i-1]所对应的最长后缀

根据next数组的含义，易知：A == B（结论1），示意图如下：

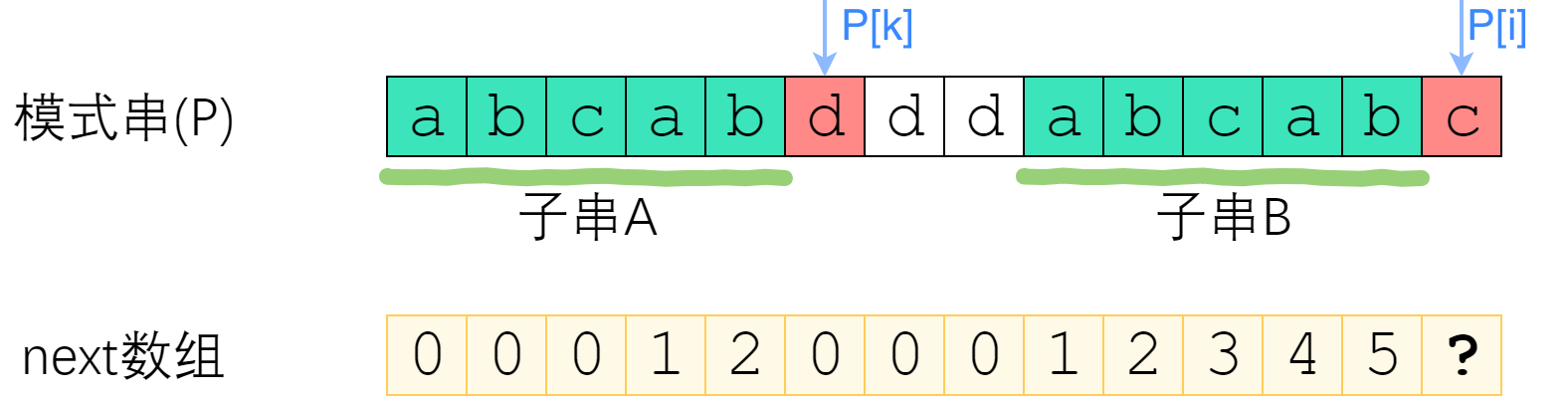子串A、B示意图

再次回顾next数组元素的含义：“前后缀相等的最大值”（结论2）。

以上是铺垫内容，下面开始介绍求解思路。

现在的已知条件是：

  • A == B，即：P[0] ~ P[k-1] == P[i-k] ~ P[i-1]
  • P[k] != P[i]，即：P[0] ~ P[k-1] + P[k] != P[i-k] ~ P[i-1] + P[i]

需要解决的问题：

  • 找到next[i] = $l$，使得：P[0] ~ P[$l$-1] == P[i-$l$+1] ~ P[i]
  • 为了找到$l$，首先需要找到m，使得：P[0] ~ P[m-1] == P[i-m] ~ P[i-1]

显然可得：

  • $ l < k $
  • $ m = l - 1$，物理含义为：P[0] ~ P[m-1]是子串A的部分前缀，P[i-m] ~ P[i-1]是子串B的部分后缀（结论3）。

因为$l$要尽可能大（结论2），所以m就要尽可能大。因此，现在要解决的问题是尽可能使m最大：

  • 通过结论1和结论3可以得到的一个洞察是：A的前m个字符 == A的后m个字符；
  • 再结合结论2，可以得到不等式m $\leq$ next[i-1]。

因此，m的最大值应为：m = next[i-1]。后续要做的：

  • 判断P[m] == P[i] ?
  • 如果相等，next[i] = m + 1
  • 如果不相等，m = next[m - 1]，重新执行判断操作

实现代码

构造Next
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void getNext(vector<int>& next, string p) {
    int len = next.size();
    next[0] = 0;
    int i = 1;
    int j = next[i-1];
    while (i < len) {
        if (p[j] == p[i]) {
            next[i++] = ++j;
        } else if (j != 0) {
            j = next[j-1];
        } else {
            next[i] = 0;
            i++;
        }
    }
}

KMP算法完整代码

KMP算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int kmpSearch(string s, string p) {
    int ret = -1;
    int s_len = s.size();
    int p_len = p.size();
    vector<int> next(p_len);
    getNext(next, p);
    int i = 0, j = 0;
    while (i < p_len && j < s_len) {
        if (p[i] == s[j]) {
            i++;
            j++;
        } else if (i != 0) {
            i = next[i-1];
        } else {
            j++;
        }
   }
   if (i == p_len) {
	 ret = j - p_len;
   }
   return ret;
}